动态规划（ dynamic programming ）算法是解决多阶段决策过程最优化问题的一种常用方法，难度比较大，技巧性也很强。利用动态规划算法，可以优雅而高效地解决很多贪婪算法或分治算法不能解决的问题。动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果，与贪婪算法不同的是，在贪婪算法中，每采用一次贪婪准则，便做出一个不可撤回的决策；而在动态规划算法中，还要考察每个最优决策序列中是否包含一个最优决策子序列，即问题是否具有最优子结构性质。

动态规划算法的有效性依赖于待求解问题本身具有的三个重要性质。

最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
无后效性，将原问题分解成若干的问题，每个子问题的求解作为一个阶段，当前阶段的求解只与之前阶段相关，与之后阶段无关。
子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的解题效率。

其实以上定义的核心就是从起点(初始状态)出发，经过一系列的子问题求解(状态转移)，到达终点(目标状态)。求解最优值，方案数，概率的问题。但需要注意的是，状态转移必须有方向，且不能成环(有向无环图)；并且状态的个数必须在可接受范围内

当我们已经确定待解决的问题需要用动态规划算法求解时，通常可以按照以下步骤设计动态规划算法：

分析问题的最优解，找出最优解的性质，并刻画其结构特征；
递归地定义最优值；
采用自底向上的方式计算问题的最优值；
根据计算最优值时得到的信息，构造最优解。

1 ～ 3 步是动态规划算法解决问题的基本步骤，在只需要计算最优值的问题中，完成这三个基本步骤就可以了。如果问题需要构造最优解，还要执行第 4 步；此时，在第 3 步通常需要记录更多的信息，以便在步骤 4 中，有足够的信息快速地构造出最优解。

动态规划中最核心的是状态转移的概念，而其中的状态可以理解成是对问题的分解的值，是一个子问题，是一个能够用数字来描述的局面对应答案的值

数塔问题

         9 
      12   15 
    10   6   8 
  2   18   9   5 
19   7   10   4   16

采用顺推或者倒推得到子问题就是求得上一级的所有可能和再加上自己

         9 
      21   24 
    31   30   32 
  33  49    41   37 
52  56   59    45   53

在这个过程中，状态转移就是

1 2	21 24 31 30 32

21（dp[i][j]）->31(dp[i+1][j])或者30(dp[i+1][j+1])的过程；局面就是i,j的数字，是整体用数字表达概览；状态就是dp[i][j]的值，就是在一个局面下对于特定问题的值。

而在状态转移的过程中，状态是在约束的情况下发生转移的这里就引入状态转移方程。

$$
f(i, j)=\left{\begin{array}{ll}
w(0,0), & i=0, j=0 \
f(i-1, j)+w(i, j), & j=0\
f(i-1, j-1)+w(i, j), & j = i \
\max {f(i-1, j-1), f(i-1, j)}+w(i, j), & \text { other }
\end{array}\right.
$$

求解

逆推

int maxSumNumberTower(vector<vector<int>>& w) {
    if (w.empty() || w[0].empty()) {
        return 0;
    }
    
    int n = w.size();
    for (int i = n - 2; i >= 0; i--) {
        for (int j = 0; j <= i; j++) {

            w[i][j] += max(w[i + 1][j], w[i + 1][j + 1]);
        }
    }
    
    return w[0][0];
}

顺推

vector<vector<int>> dp(n,vector<int>(n));
for(int i = 0;i<=n;i++){
    for(int j = 0;j<=i;j++){
        if(i == 0) dp[i][j] = w[i][j];
        else if(j == 0) dp[i][j] = dp[i-1][j]+w[i][j];
        else if(j == i) dp[i][j] = dp[i-1][j-1]+w[i][j];
        else dp[i][j] = max(dp[i-1][j-1]+w[i][j],dp[i-1][j]+w[i][j];)
    }
}
cout<< *max_element(dp[n-1].begin(),dp[n-1].end())<<endl;

记忆化递归

vector<vector<int>> dp(n,vector<int>(n,-1));

auto dfs = [&](auto& self,int i,int j){
  auto &res = dp[i][j];
  if(res!=-1) return res;
  if(i == 0) return res = w[0][0];
  if(j == 0) return res = self(self,i-1,j)+w[i][j];
  if(j == i) return res = self(self,i-1,j-1)+w[i][j];
  return res = max(self(self,i-1,j-1),self(self,i-1,j)+w[i][j]);
};
int ans = 0;
for(int j = 0;j<n;j++){
  ans = max(ans,dfs(dfs,n-1,j));
} 
cout<<ans;

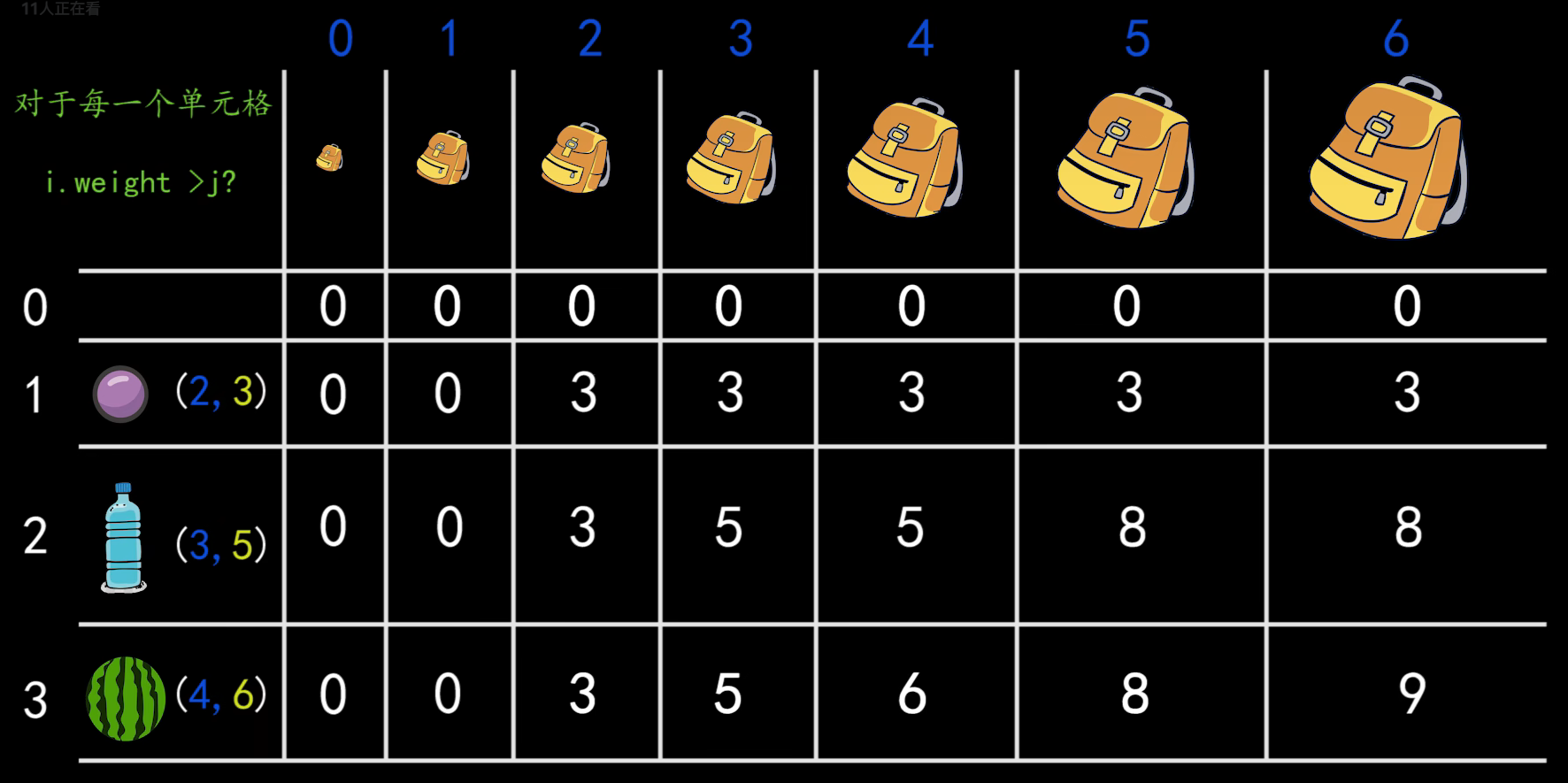
01背包问题

葡萄重量为2，价值为3；矿泉水重量为3价值为5；西瓜重量为4，价值为6。背包容量为6考虑如何填充背包使价值最大。不可以重复装同一物品。

在这个判断过程中，就是在当前行判断能否装下这个物品，并于同列上一行进行比较，判断取那个值作为当前格子的最优解。判断最优解的过程就是状态转移过程。

求解

int DP_2(int capacity,const vector<int>& weights,const vector<int>& values){
  int n_items = weights.size();
  if (n_items == 0) {
      return 0;
  }
  std::vector<std::vector<int>> dp(n_items + 1, std::vector<int>(capacity + 1, 0));//多“0”行和列
  for(int i = 0,i<n_items;i++){
      int current_weight = weights[i];
      int current_value = values[i];
      for(int j = 0;j <= capacity;j++){
        if(j<current_weight) {
            // 当前背包容量装不下第 i 个物品，只能选择不装
            dp[i+1][j] = dp[i][j];
        } else {
            // 在“不装”和“装”之间做选择
            // 1. 不装第 i 个物品: dp[i-1][j]
            // 2. 装第 i 个物品: dp[i-1][j - current_weight] + current_value
            dp[i+1][j] = std::max(dp[i][j], dp[i][j - current_weight] + current_value);
        }
      }
    }
    return dp[n_items][capacity];
}

int DP_1(int capacity, const std::vector<int>& weights, const std::vector<int>& values) {
    int n_items = weights.size();
    if (n_items == 0) return 0;
    std::vector<int> dp(capacity + 1, 0);
    for (int i = 0; i < n_items; ++i) {
        int current_weight = weights[i];
        int current_value = values[i];
        for (int j = capacity; j >= current_weight; --j) {
            dp[j] = std::max(dp[j], dp[j - current_weight] + current_value);
        }
    }
    return dp[capacity];
}